2. Conjunção

A segunda coisa que corri atrás de aprender foi estudar essa tal de conjunção. Mas agora não foi tão difícil entender esse negócio depois de ter estudado disjunção no capítulo anterior,

segue link: https://profservulo.wixsite.com/meusestudos/blog/1-disjun%C3%A7%C3%A3o

Como o próprio nome já diz, ao pé da letra, conjunção significa juntar, unir, ligar. É o contrário do que vimos no capítulo 1 sobre disjunção.

Duas ou mais estradas se tornando uma única é uma analogia perfeita para esse caso. ^

Buscando a lógica de tal, lembrei que disjunção significa 'separação'... Poxa vida, então conjunção e disjunção são meio que opostas, não é isso?! Se eu não estiver junto é porque está separado, e vice-versa. E lembrei também que simbolicamente usa-se " v " para indicar disjunção (pode ser usado também o "ou"), o que faz total sentido se observarmos de baixo para cima este símbolo, pois nota-se que parece um caminho se tornando dois.

Então pensa aí como seria uma boa maneira de representar a nossa querida novata CONJUNÇÃO!

O oposto disso, não é? Então que símbolo seria legal e lógico para representarmos a conjunção? Como significa juntar, duas coisas se tornam uma única, é bem lógico simbolizarmos por " ^ ", que é justamente o contrário do outro " v ".

Imaginemos em uma situação prática. Lembra aquele exemplo da estrada do capítulo anterior (cap. 1)? Aquele exemplo que você está em uma pista perfeita, retinha, e você se deparava em dois caminhos para você seguir. Pronto! Pensemos como conjunção o contrário disso. Você tem dois (ou mais) caminhos que vira um único. Como são dois caminhos, coloquemos então uma pessoa em cada uma dessas estradas. Por exemplo Pedro e João. O objetivo é se encontrarem na estrada única lá na frente, onde as duas se encontram. Se uma dessas estradas tiverem interrompidas, ou seja, F (falsa), eles não vão se encontrar. Só se encontram em uma única situação: quando as duas estradas estiverem livres e podendo passar, ou seja, V (verdade). Caso ocorra de alguma estrada estar interrompida (na linguagem lógica, F) não se encontrarão, portanto resultando em F.

Observe a tabela que tanto as pessoas decoram como faz todo sentido agora.

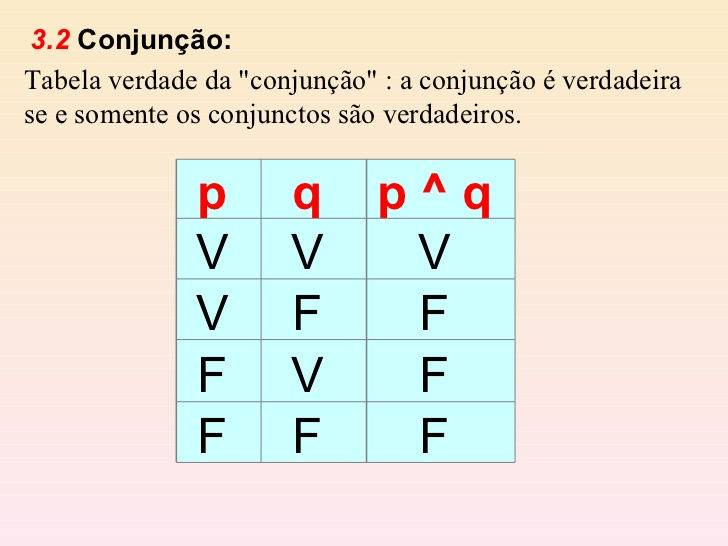
-Na primeira linha ocorre de as duas estradas estarem livres, resultando no encontro dos dois, ou seja, em V ( V ^ V = V).

-Na segunda linha a primeira está boa, mas a segunda não, então não se encontrarão, portanto F (V ^ F = F).

-Na terceira linha a primeira está ruim e a segunda boa, ou seja, não se encontrarão também, portanto F (F ^ V = F).

-A última as duas estão ruins, então não se encontrarão também, portanto F também ( F ^ F = F).

Perceba que a dedução disso é que para ser V ambas têm que estar V, ou seja, a primeira V e a segunda V. V e V = V.

Pode-se se simbolizar o " ^ " também como o " e ". Tanto faz dizer p e q como p ^ q.

Note que:

As proposições simples que tanto estudam é como se fosse a estrada. Se temos duas proposições (p e q) temos que saber o que vai ocorrer entre elas, se uma conjunção ( ^ ) ou uma disjunção ( v ).

Vejamos alguns exemplos:

exemplo 1:

p ^ q , onde os valores lógicos são: p = V; q = F

resolução:

Aí entre as letras tem o símbolo da conjunção ( ^ ).

Então ambas as estradas têm que estar livres (V) para poderem se encontrar.

A primeira p é V, a segunda q é F, portanto o resultado é F, pois uma das estradas está F (fechada).

exemplo 2:

p ^ q , onde os valores lógicos são: p= V; q = V

resolução:

Aí também trata-se de conjunção ( ^ ) entre as estradas p e q.

Como ambos possuem valores lógicos V, o resultado disso é V.

Exemplo 3:

p v q , onde os valores lógicos são p = V; q = F

resolução:

Aí trata-se de disjunção ( v ), do capítulo anterior (cap. 1).

Como uma das estradas está perfeita (V) então conseguiremos chegar ao destino.

Concluindo então que o valor lógico resultante é V.

Pronto! É isso!

Segundo capítulo cumprido e visando os próximos para dominar esse raciocínio lógico.

Próximos capítulos...

4. Condicional

5. Bicondicional

6. Disjunção Exclusiva

7. Exercícios

...